
Los Árboles son las estructuras de datos mas utilizadas, pero también una de las mas complejas, Los Árboles se caracterizan por almacenar sus nodos en forma jerárquica y no en forma lineal como las Listas Ligadas, Colas,Pilas,etc., de las cuales ya hemos hablado en días pasados.
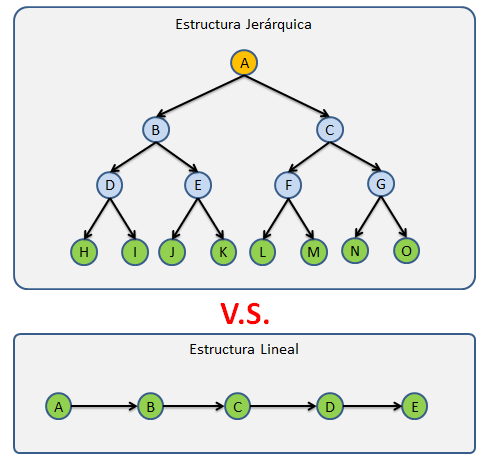
Datos importantes de los Árboles
Para comprender mejor que es un árbol comenzaremos explicando como está estructurado.
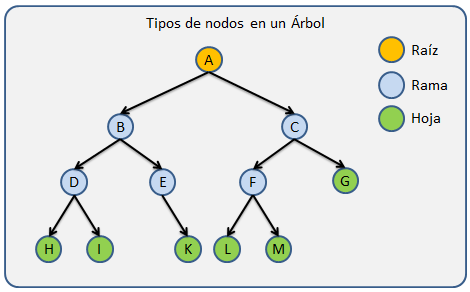
Nodos: Se le llama Nodo a cada elemento que contiene un Árbol.
Nodo Raíz: Se refiere al primer nodo de un Árbol, Solo un nodo del Árbol puede ser la Raíz.
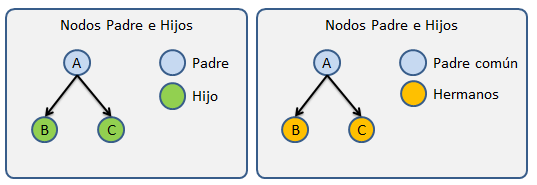
Nodo Padre: Se utiliza este termino para llamar a todos aquellos nodos que tiene al menos un hijo.
Nodo Hijo: Los hijos son todos aquellos nodos que tiene un padre.
Nodo Hermano: Los nodos hermanos son aquellos nodos que comparte a un mismo padre en común dentro de la estructura.
Nodo Hoja: Son todos aquellos nodos que no tienen hijos, los cuales siempre se encuentran en los extremos de la estructura.
Nodo Rama: Estos son todos aquellos nodos que no son la raíz y que ademas tiene al menos un hijo.
Los arboles a demas de los nodos tiene otras propiedades importantes que son utilizadas en diferente ámbitos los cuales son:
Nivel: Nos referimos como nivel a cada generación dentro del árbol. Por ejemplo, cuando a un nodo hoja le agregamos un hijo, el nodo hoja pasa a ser un nodo rama pero a demas el árbol crece una generación por lo que el Árbol tiene un nivel mas.Cada generación tiene un número de Nivel distinto que las demas generaciones.
- Un árbol vacío tiene 0 niveles
- El nivel de la Raíz es 1
- El nivel de cada nodo se calculado contando cuantos nodos existen sobre el, hasta llegar a la raíz + 1, y de forma inversa también se podría, contar cuantos nodos existes desde la raíz hasta el nodo buscado + 1.
Altura: Le llamamos Altura al número máximo de niveles de un Árbol.
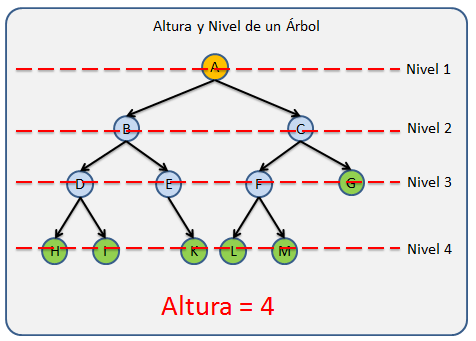
La altura es calculado mediante recursividad tomando el nivel mas grande de los dos sub-árboles de forma recursiva de la siguiente manera:
altura = max(altura(hijo1), altura(hijo2),altura(hijoN)) + 1
Peso: Conocemos como peso a el número de nodos que tiene un Árbol. Este factor es importante por que nos da una idea del tamaño del árbol y el tamaño en memoria que nos puede ocupar en tiempo de ejecución(Complejidad Espacial en análisis de algoritmos.)
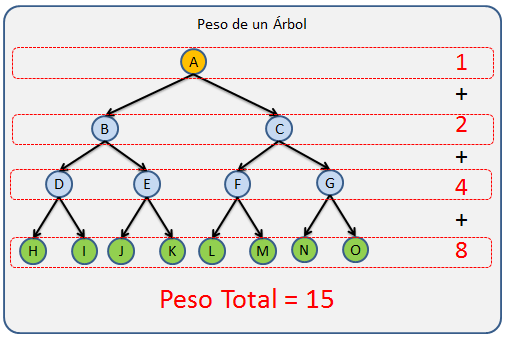
El peso se puede calcular mediante cualquier tipo de recorrido el cual valla contando los nodo a medida que avanza sobre la estructura. El peso es un árbol es igual a la suma del peso de los sub-árboles hijos + 1
peso = peso(hijo1) + peso(hijo2) + peso(hijoN)+ 1
Nota: Los tipos de recorridos los veremos mas adelante.
Orden: El Orden de un árbol es el número máximo de hijos que puede tener un Nodo.

Notemos que un Árbol con Orden = 1 no tendría sentido ya que seria una estructura lineal. ya que cada nodo solo podría tener un Hijo y tendríamos un Árbol como la Imagen de la Fig.1.
Este valor no lo calculamos, si no que ya lo debemos conocer cuando diseñamos nuestra estructura, ya que si queremos calcular esto lo que obtendremos es el grado(hablamos de el continuación).
Grado: El grado se refiere al número mayor de hijos que tiene alguno de los nodos del Árbol y esta limitado por el Orden, ya que este indica el número máximo de hijos que puede tener un nodo.
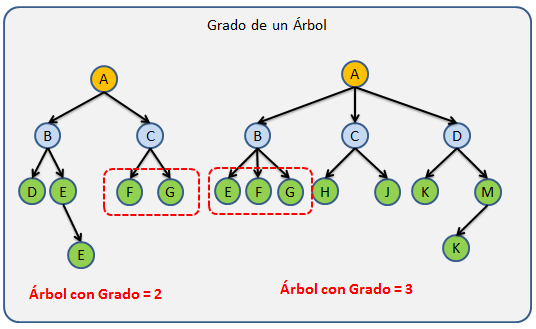
El grado se calcula contando de forma recursiva el número de hijos de cada sub-árbol hijo y el numero de hijos del nodo actual para tomar el mayor, esta operación se hace de forma recursiva para recorrer todo el árbol.
grado = max(contarHijos(hijo1),contarHijos(hijo2), contarHijos(hijoN), contarHijos(this))
Sub-Árbol: Conocemos como Sub-Árbol a todo Árbol generado a partir de una sección determinada del Árbol, Por lo que podemos decir que un Árbol es un nodo Raíz con N Sub-Árboles.

Existen escenarios donde podemos sacar un Sub-Árboles del Árbol para procesarlo de forma separada, de esta forma el Sub-Árboles pasa a ser un Árbol independiente, También podemos eliminar Sub-Árboles completos, Agregarlos,entre otras operaciones.
Árbol n-ario
los arboles n-arios son aquellos arboles donde el número máximo de hijos por nodo es de N, en la figura 7 podemos apreciar dos árboles con grado 2 y grado 3, estos dos arboles también los podemos definir como Árbol n-ario con n = 2 y n=3 respectivamente.
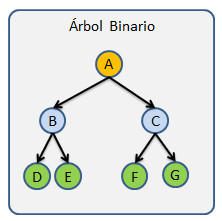
Árboles binarios
Esta estructura se caracteriza por que cada nodo solo puede tener máximo 2 hijo, dicho de otra manera es un Árbol n-ario de Grado 2.
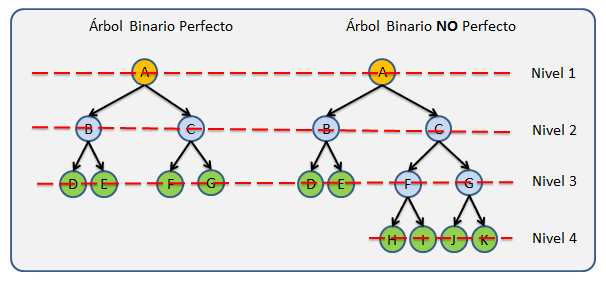
Árbol binario lleno: Es aquel que el que todos los nodos tiene cero o 2 hijos con excepción de la Raíz.
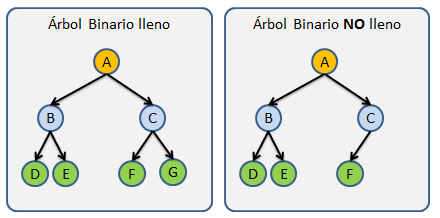
Árbol binario perfecto: Es un Árbol lleno en donde todos las Hojas están en el mismo Nivel.
Recorrido sobre Árboles
Los recorridos son algoritmos que nos permiten recorrer un árbol en un orden especifico, los recorridos nos pueden ayudar encontrar un nodo en el árbol, o buscar una posición determinada para insertar o eliminar un nodo.
Básicamente podemos catalogar las búsqueda en dos tipos, las búsqueda en profundidad y las búsquedas en amplitud.
Búsquedas no informadas
Las búsquedas no informadas son aquellas en que se realiza el viaje por todo el árbol sin tener una pista de donde pueda estar el dato deseado. Este tipo de búsquedas también se conocen como búsquedas a ciegas.
Para comprender mejor que es una búsqueda no informada expondremos el siguiente ejemplo:
Imagine que vamos por la carretera y de repente encontramos dos caminos, el problema a qui es que uno después de 50 kilómetros esta en construcción y el otro nos lleva a nuestro destino, sin embargo ninguno de los caminos tiene señalamiento. Lo que tendríamos que hacer es recorrer el primero camino y después de 50 kilómetros encontrarnos con que el camino esta en construcción, entonces tendríamos que regresar para irnos por el segundo camino,el cual nos lleva a nuestro destino(Para esto ya recorrimos los 50 kilómetros de ida y los 50 kilómetros de regreso lo que nos da 100 kilómetros mas a nuestra ruta).
A este tipo de escenarios en los cuales las búsquedas de hacen a ciegas los conocemos como búsquedas no informadas.
Las siguientes métodos de búsqueda que veremos a continuación(Búsqueda en profundad y Búsqueda en amplitud) pertenecen a las búsquedas no informadas.
Búsqueda en profundidad
Recorrido Pre-orden: El recorrido inicia en la Raíz y luego se recorre en pre-orden cada unos de los sub-árboles de izquierda a derecha.
Esta definición puede ser un poco compleja de entender por lo que mejor les dejo la siguiente imagen.
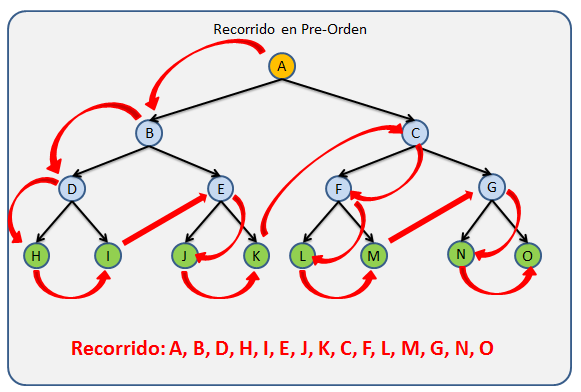
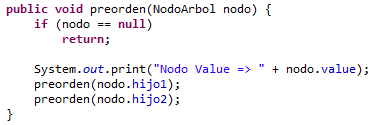
Recorrido Pos-orden: Se recorre el pos-orden cada uno de los sub-árboles y al final se recorre la raíz.
Para comprender mejor esta definición observemos la siguiente imagen:
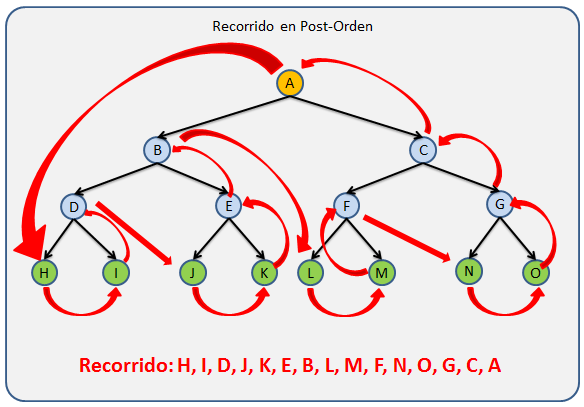

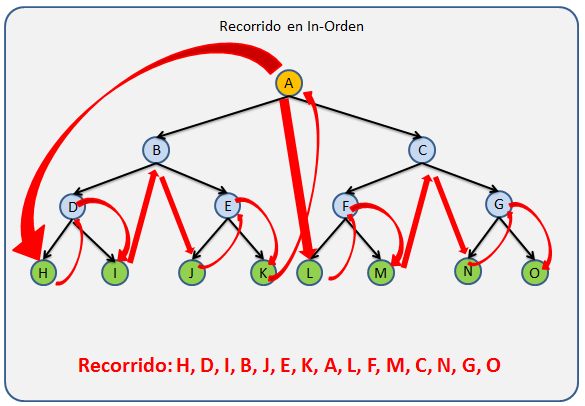
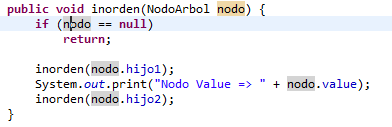
Recorrido in-orden: Se recorre en in-orden el primer sub-árbol, luego se recorre la raíz y al final se recorre en in-orden los demas sub-árboles
Búsqueda en amplitud.
Se recorre primero la raíz, luego se recorren los demas nodos ordenados por el nivel al que pertenecen en orden de Izquierda a derecha.
Este tipo de búsqueda se caracteriza por que la búsqueda se hace nivel por nivel y de izquierda a derecha.
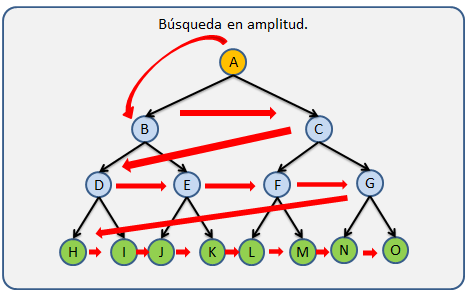
En la imagen podemos observa que el árbol es recorrido en su totalidad pero esto no siempre es a sí, ya que el algoritmo se detiene cuando el elemento buscado es encontrado.
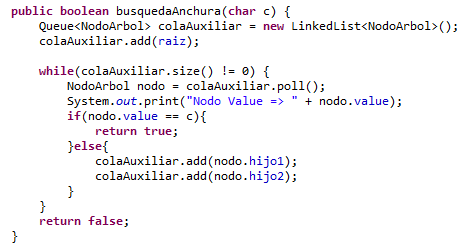
Si observamos el código de forma minuciosa podemos observar dos puntos muy interesantes, el primero es que esta función no es recursiva, y la segunda es que se utiliza una Cola para controlar el flujo del recorrido.
Los pasos para hacer el recorrido es el siguiente:
- Se agrega la Raíz a la cola de nodos por visitar
- Mientras que la cola no este vacía se saca el primer elemento de la cola y continuamos con el paso 3, Pero; si la cola esta vacía entonces nos vamos al paso 5.
- Se valida si el elemento sacado de la pila es el que estamos buscando, Si lo es, entonces hemos terminado, Si no lo es se agregan todos los hijos del nodo a la pila de nodos pendientes por procesar.
- Regresamos al paso 2.
- Terminamos sin un resultado.
Conclusiones
Como hemos observado los arboles son estructuras bastante complejas, tiene una gran aplicaciones en la ciencia y en la programación convencional. En los últimos años este tipo de estructuras ha sido utilizadas con mucha frecuencia en la Inteligencia artificial.
En esta publicación hemos visto los puntos vas relevantes a en cuenta a lo que son los arboles y los principales métodos de búsqueda, sin embargo estamos lejos de cubrir este tema en profundidad ya que existen muchísimos tipos de operaciones y algoritmos que se pueden realizar sobre estas estructuras de datos.
Espero que este información te sirve de utilidad y no olvides darle like y recomendar esta publicación ya que esto me servirá para crear mas y mejor material.

muy interesante, me gustaria saber si es posible que una funcion podria devolver la cantidad de nodos en un nivel..
Hola Matias, claro que es posible, eso lo lo logras con las “busquedas en amplitud”, este es un algotimo que analiza el arbol por niveles, y en cada nivel podriss recuperar el numero de nodos
Se podrían implementar un árbol con listas doblemente ligadas?
Respondo a tu comentario en la pregunta que formulaste primero.
Con respecto a la altura de un árbol he observado en otras fuentes que el nivel empieza desde 0 y la altura del árbol del ejemplo sería 3
Excelente explicación..sabes como podria pintarlo en pantalla…? Es decir como imprimir el arbol gráficamente?
Yo te recomiendo que busques un librería que lo haga por ti en el lenguaje que estás utilizando, ya hay muchos desarrollados, por lo que no tiene caso que te preocupes por dibujarlo tu mismo.
Excelente trabajo. Felicidades
Gracias por el comentario 🙂
Como se podría implementar el árbol con listas doblemente ligadas? Espero puedan ayudarme
Hola amigo, por la forma en que preguntas me suena a que te lo dejaron de tarea jejeje,
Ahora bien, respondiendo tu pregunta, una lista ligada o doblemente ligada es un estructura de datos lineal, a diferencia del árbol donde cada nodo puede tener muchos hijos, dicho esto, es un poco extraño que preguntes si puedes implementar un árbol con listas ligadas, sin embargo, si analizamos como se conforma un árbol, es de cierta forma una lista doblemente ligada, por que cada nodo tiene un referencia a su padre (nodo anterior) y a los hijos (nodos siguientes), con la única diferencia de que la raíz no tiene nodo padre (nodo anterior) y las hojas no tiene nodos hijos (siguientes), por lo tanto, la característica de ciclisidad (el último nodo a punta al primero) no se puede dar en un árbol.
Espero haber resuelto tu duda.
Gracias por la información, me ha sido de mucha utilidad ojala siga sacando este tipo de contenido. Saludos.
Gracias por el comentario Moises, y me alegro que el contenido sea de utilidad.
Hola buenas noches yo creo un sistema de árbol binario pero la verdad no me brindó buenos resultados por no tener una base sólida de pronto yo podría vender este sistema binario que fue realizado por expertos en html, como podría yo vender este tipo de sistema tú podrías brindarme alguna recomendación y si tendrías un cliente que este interesado podríamos llegar a un acuerdo entre el presupuesto que ganarías tu por conseguir este cliente. La verdad te felicito muchos éxitos, toda esta explicación ayuda mucho.
Hola Patricia, que pena, pero no tengo ninguna persona que de repente este interesada en algo así
hola me podrías responder estas preguntas:
¿Cuál es la estructura de datos que se indiza en O(1)?
Cola basada en lista enlazada Lista enlazada Árbol Array Diccionario con array
Buscar un elemento en un array es
O(1) O(n2) O(n logn) O(n)
gracias
Hola Rossmery, no entendí tu pregunta, podrías ser un poco más clara?
saludos.
Hola, si son dos preguntas es decir
1. ¿Cuál es la estructura de datos que se indiza en O(1)?
cual seria la respuesta de las que me dan:
-Cola basada en lista enlazada
-Lista enlazada
-Árbol
-Array
-Diccionario con array
y la otra pregunta igual
Buscar un elemento en un array es
O(1)
O(n2)
O(n logn)
O(n)
cual de las posibles respuesta es la correcta.
gracias
Hola Rossmary, esas preguntas están engañosas, por que la Notación asintótica no solo depende de la estructura de datos, si no el algoritmo que utilices para recorrerlo o buscar un elemento, por ejemplo, no es lo mismo buscar un elemento en un array de forma lineal que hacer una búsqueda binaria.
jaja me lo dices a mi, es un cuestionario que tengo que responde en clases y la verdad no tengo ni idea. gracias de todos modos.
jajaja, bueno, es que eso que te menciono es como funciona, que te puedo decir jejej
¿tendras el codigo? me salvarias la vidaaa no entiendo unos metodos
Hola Pablo, no hay código de eso, solo es la teoría, es decir, el código que sale allí es la esencia, pero no tengo un programa como tal
Hola,
Encontré tu información y veo que entiendes muy bien, ya que las explicaciones son excelentes.
Soy totalmente nuevo en este tema y la parte conceptual la entiendo, solo necesito algunas recomendaciones para la parte práctica:
1- para implementar ya no necesito escribir código , porque ya hay librerías cierto? Si esto es verdad ? En c cual librería me recomiendas usar
2- el lenguaje más simple para hacer lo anterior es c o podrías recomendarme otro (phyton p en)
3. Empecé a leer algunos libros, pero son muy teóricos, hay algún libro para dummies que sea muy práctico-teorico
Saludos
Hola Felix, en realidad yo conozco mucho de C, sin embargo, todos los lenguajes tiene librerías para trabajar con Árboles, sin embargo, es muy probable que tengas que programar mucho, pues las librerías son más que nada para crear la estructura y realizar una que otra operación sobre el árbol, sin embargo, tendrás que programar la lógica específica de lo que quieras hacer.
Con respecto a tu segunda pregunta, yo creo que ha de ser muy similar en todos los lenguajes, lo único que puede hacer la diferencia es que tal familiarizado estés con un determinado lenguaje.
Respecto a tu tercer pregunta, no conozco un libro que trate meramente de árboles, si que más bien este tema se cubre en libros de algoritmia, o AI, por lo que puedes buscar en amazon varias opciones
saludos
Muy buen artículo. Muchas gracias por compartir.
Gracias por el comentario Xavi. saludos.
Muy bueno el artículo, explica todo a detalle y es muy fácil de entender. La verdad me van a servir para mis clases de Base de Datos. Saludos y nuevamente muchas gracias por la información
Hola Miguel, que bueno que te sirvió el artículo.
De maravilla, pero lo que tengo duda es si existe algún código para hacer eso en C# con la plataforma de Visual Studio, es que estuve buscando y no encontré, no sé si sepas de alguna pagina o algo así y la verdad me serviría muchísimo y nuevamente muchas gracias.
Hola Miguel, la verdad desconozco de algo en C#, como verás, no es un lenguaje que yo utilice, por lo tanto, no estoy muy al tanto.
saludos.
Buen trabajo. Al grano, claro, con implementaciones en c# y bonitas imagenes . Los árboles se usan para infinidad de cosas en programación, yo no dejo de usarlos. minmax, A*,redes neuronales, xml…
*System.out.print() java XDD
Jajaj, es Java en realidad, pero prácticamente es lo mismo
Si, lo árboles son de las estructuras de datos más utilizadas, pero también son de las más complejas.
una consulta, podrias indicarme un link o bien algun articulo donde pueda obtener informacion detallada de la informacion que brindan los arboles binarios, tales como:
o Comprobar si un árbol está vacío.
o Calcular el número de nodos.
o Comprobar si el nodo es hoja.
o Calcular la altura de un nodo.
o Calcular la altura de un árbol.
He estado buscando informacion pero no logro encontrar algun articulo que responda a esto, desde ya muchas gracias, me fue muy util la informacion que encontrè en esta web
No tengo una página como tal, pero yo en tu lugar buscaría un libro de estructuras de datos o algoritmos, esos libros cubren muy bien los árboles
Muy buena publicación, me sirvió de mucho Gracias sigue así.
Gracias Ricardo 🙂
Excelente trabajo!!!
Gracias por el comentario Esther, saludos.
Podría dar un ejemplo de alguna aplicación práctica de los árboles en la programación cotidiana por ejemplo:un algoritmo de búsqueda, minería de datos o algo por el estilo es que siempre me he preguntado como programador donde lo aplicaría.
Pues un ejemplo simple y claro, son los menús de la interface gráfica en forma de árbol, incluso, los submenús, por dentro son un árbol, pero también tiene aplicaciones en las búsquedas de profundidad, ordenamiento de elementos, etc. los árboles tiene su principal funcionalidad en los algoritmos, es por ello que casi no los ves en la programación de aplicaciones tradicionales.
Muchas gracias por tu respuesta y gracias por compartir tu conocimiento quedo muy agradecido
Por nada Armando 🙂
Hola, tengo un proyecto personal de java en mente, alguien me podría indicar cómo dividir un “árbol binario perfecto de nivel 2” en dos arboles binarios luego de que el árbol este lleno cuando se le agregue el nodo “hoja O” , para ahora pasar a ser dos arboles en el que ahora sus padres sean las “ramas B y C” ? Agradezco cualquier ayuda o sugerencia abnerlr89@gmail.com
Hola Abner, no puedo darte una respuesta concreta a esta respuesta, pues no conozco exactamente el problema a resolver, pero te diría que podría recorrer el árbol e ir separando los nodos, o si ya lo tienes dentro de una estructura, podrías tomar un sub-árbol y convertirlo en un árbol por si mismo. Es lo que se me ocurre a sí de rápido sin tener contexto del problema a resolver.
Hola, como podría armar un árbol a partir de sus recorridos?
Te refieres a crear un nuevo árbol recorriendo uno existente?
Si esa es tu pregunta, no existe una forma única, pues depende como quieras crear el nuevo árbol, en que orden, que elementos, etc.
como puedo crear un metodo o algoritmo para saber si dos o mas arboles son semejantes
pregunta repetida, revisa mi respuesta anterior.
como hago para crear un algoritmo o metodo para arboles binarios de busqueda que me permita determinar si dos o mas arboles son semejantes
Hola, no conozco el contexto de tu aplicación ni la estructura en la cual tienes almacenada la estructura de árbol, pero dado lo que me dices, yo lo que aria fuera realizar un recorrido en pre-orden y almacenar los valores en un array, de esta forma tendría dos arrays, lo siguiente sería hacer dos
foranidados (uno para cada árbol) y luego comprar elementos por elemento, de esta forma, en cuanto un elemento no coincide con el otro, puedo hacer un break y no tengo que comprar todos los elementos, haciendo más efectivo el algoritmo.saludos
Hola, me puedes decir como hago un algoritmo para la reconstrucción de un árbol mediante 2 recorridos
no entiendo, para que quieres reconstruir de un arbol con 2 recorridos? por que dos recorridos? no entiendo
Hola, me puedes facilitar el con el código de su ejemplo me seria de gran ayuda es que debo adapto el código de jarras al de búsqueda por anchura y profundidad y la verdad su publicación es muy bueno ante mano felicidades recomendare esta publicación en mi salón de clases.
Hola Gustavo, hace mucho de crees este artículo y la verdad es que no conservé el código, además, la teoría que hay aquí debería ser suficiente como para que lo puedas reproducir.
Saludos
Hola como puedo crear una funcionalidad recursiva que permita encontrar el promedio y la desviación estándar de los elementos del árbol.
La formula de la desviación estándar:
√ ∑(x-x)^2/(n-1)
Hola Juan, lo se me ocurre es que hagas cualquier recorrido sobre el árbol, ya sea en in-orden, pre-orden, pos-orden, sumes los elementos y al final obtendrás el promedio, de la misma forma, puedes ir calculando la desviación estándar.
saludos.
hola como puedo implementar un método recursivo que permita determinar si dos nodos del árbol son hermanos.
Hola Andres, si tu input son los dos nodos, ni siquiera requieres de un algoritmo, pues un nodo es un objeto que contiene el payload(dato) la referencia a los hijos y la referencia al padre, en tal caso, solo basta con comparar el padre de los dos nodos para saber si comparten el mismo padre, en tal caso, son hermanos.
saludos.
Hola como puedo hacer los recorridos de preorden inorden postorden en un arbol n ario y retornar los nodos de un nivel….
Si lo que necesitas es retornar los nodos de un nivel, el algoritmo inorden, postorden y preorden no son nada efectivos, pues tendrás que recorrer nodos innecesarios, en tu lugar, yo utilizará una búsqueda en anchura, para la cual es necesario utilizar una Queue (cola), no tengo un artículo que hable del tema, pero te sugiero que lo busques en internet, verás que es muy fácil.
Hola como hago un sistema de archivos con arboles n arios y recorridos
wow wow wow, tranquilo amigo, me estás pidiendo que te diga como programa todo eso, te puedo ayudar a resolver dudas puntuales, pero lo que me pides es que te diga como programar un “sistema de archivos”, lo que te puedo decir es que aprendas bien el concepto de recursividad, pues lo vas a necesitar mucho, por otro lado, no se ni como responderte la duda, por que es muy abstracta, quizás si me haces una pregunta más concreta te pueda ayudar. saludos.
hola!!
¿Cuál considera que es la diferencia más importante entre Árboles y Árboles Binarios?.
espero su comentario…..gracias.
Hola Nidia, Árboles es la forma genércia de mencionar a la estructura de datos, mientras que un Árbol binario es un tipo de árbol en donde cada nodo puede tener máximo dos hijos
Hola amigo, te queria pedir ayuda , ya que sabes bastante del tema… Por casualidad tienes ideas de como utilizar arboles en un proyecto final? Necesito ideas urgentemente, nose como aplicarlo…. Gracias por ensenar con tu blog.
Puedes utilizar arboles para hacer búsqueda binarias, es decir, puedes crear un programa al cual le puedas agregar una serie de número, el cual los va colocando ordenadamente en el árbol de forma ordenada, luego, le puedes pedir que te busque un numero, utilizando búsqueda binaria. Este es un tema muy complejo de explicar un comentario, pero te dejo la siguiente liga donde lo explican muy bien: http://decsai.ugr.es/~jfv/ed1/tedi/cdrom/docs/arb_BB.htm
EXCELENTE! muy bien explicado
Gracias por tu comentario. saludos
Hola Oscar
Muy buena tu explicación.
Tengo un objeto el cual se inicia con una clase principal, la cual contiene propiedades, algunas apuntan a otras clases, otras son listas que a su vez pueden contener listas.
Necesito recorrer todo el objeto en su totalidad, para analizar cada propiedad independientemente de la cantidad de nodos del cual se conforme. Creo que se debe resolver con una programación recursiva. Estoy intentando hacer algo en c# pero me esta costando mucho. Sabes si hay algo de código para descargar de internet ?? saludos
Daniel
Hola Daniel, por lo que me comentas, te puede servir implementar el patrón de diseño Visitor, el cual es un patrón de diseño que permite recorrer toda la estructura de un objeto propiedad por propiedad y hacer algo mientras se recorre. El patrón lo explico a la perfección en mi libro de patrones de diseño, por si te interesa adquirirlo o buscar la información por internet, liga al libro: https://reactiveprogramming.io/books/design-patterns/es
Otra alternativa que es mucho más complicada es, utilizar Reflection, el cual es una propiedad del lenguaje para analizar la estructura de los objetos en tiempo de ejecución, te remiendo utilizar esta alternativa solo si dominas perfectamente el lenguaje por su grado de complejidad.
saludos.
muchisimas gracias por la info saludos
Gracias por el comentario Daniel 🙂
Hola necesito armar un arbol de probabilidades para un juego de cartas… son 6 cartas por jugador y juegan dos jugadores .. me podrías ayudar dandome algúna idea como hacerlo?
cual es el método que cuente cuántas hojas pares tiene un árbol binario?
Hola Yoselin, tendrías que hacer una recorrido de todo el árbol e ir validando hoja por hoja cual es par. Puede usar un recorrido post-orden, pre-orden o in-order.
saludos.
Buen aporte Oscar, habra la posibilidad de un tutorial de arboles n-narios?
Hola Ricardo, no lo sé, de momento no lo tengo en mente, pero quizás más adelante.
Aclaro que cada jugador en su turno juega una carta sola … gracias
AYUDA! CONSEJOS IDEAS PARA IMPLEMENTAR ESTE PROGRAMA. .. DESDE YA MUCHAS GRACIAS
1 se dispone de un mazo con 12 cartas numeradas de 1 a 12 que se reparten en
cantidades iguales y de manera aleatoria entre 2 jugadores.
2. El juego fija un límite máximo del cual los jugadores no pueden pasarse.
3. Los jugadores juegan una vez por turno y en cada uno se tiene que descartar una
carta.
4. El descarte va formando un montículo cuyo valor es la suma de las cartas que lo
integran. El montículo de descarte inicialmente está vacío y su valor es 0.
5. El jugador que incorpore la carta al montículo que haga que el valor del mismo supere
el límite fijado es aquel que pierde el juego.
El juego debe estar construido de tal manera que uno de los jugadores posea inteligencia
artificial y el otro le solicite la carta a jugar al usuario.
Lo han contratado a Ud. para implementar un oponente con inteligencia artificial que esté
basado en árboles MiniMax.
Los requisitos definidos para el desarrollo de su tarea son los siguientes:
1. Inicialización: Al momento de iniciado el juego se deberá construir el árbol MiniMax
que contendrá todos los posibles estados del juego.
2. Comenzar un nuevo juego: Se deberá permitir comenzar y desarrollar una nueva
partida contra el oponente con inteligencia artificial siempre que el usuario del juego
lo desee.
Amigo, no tengo idea de como ayudarte, no se exactamente que es lo que quieres implemenetar ni la sección exacta del requerimiento sobre la cual está la duda
Excelente trabajo! Muy didáctico!!
Gracias Andrés 🙂
Buenas el tipo de estructura de un árbol ¿como se implementaría en Programación Orientada a Objetos?
Hola Ariel, básicamente son objetos llamados Nodos, lo cuales pueden tener 0 o más hijos de su mismo tipo, es decir, un Tipo “Nodo” el cual puede tener referencia otros “Nodos”, los cuales a su vez, tiene más nodos. esa característica hace que la estructura crezca como un Árbol.
Saludos
Saludo y gracias muy interesante todo lo mostrado
podrias despejarme un par de dudas? soy nuevo en programacion
cuando tengo nodos con varios atributos como ser dato y color (pudiendo solo ser uno entre 2 colores) como seria el metodo para mostrar solo los nodos del color correspondiente?
Hola Marcos, dado un árbol ya formado, puedes utiliza cualquier algoritmo de recorrido de árboles para recorrerlo y comprar el color del nodo con el buscando, en tal caso podrías utiliza un recorrido en post-orden, pre-orden o in-order, cualquier te podría funcionar.
¿Los recorridos en que lenguaje lo trabajas?
Hola Ivan, los ejemplos que ves en esta artículo son en Java, aun que la teoría de árboles aplica igual en cualquier lenguaje, por lo que lo podrías aplicar esta misma lógica en cualquier lenguaje.
una pequeña pregunta.. supongamos que quiero encontrar un nodo en particula del metodo de busque de amplitud… como puedo hacer que avance la busqueda aun cuando hay ramas vacias.
me refiero a ramas vacias , cuando meto un random y me llene los espacios al antojo del mismo random, ya que es random no va a meterlos de forma binaria
mmmmm, tu pregunta es confusa, una rama por definición es un nodo que tiene al menos un hijo, por lo tanto no puede estar vació, por otro lado, el echo de que sea binario o no, no afecta la forma en que el árbol se recorre, pues al final el agoritmo recorre todos el árbol, hasta que llega a una instrucción de salida.
Buenas tardes una pregunta en un sistema que seria mas eficiente guardar la informacion en lista o en arboles?
Cual seria la mejor opcion , muy buena tu pagina me encanto
Hola Sebastian, no puedo responder tu pregunta por que no tiene sentido, cada estructura se usa para ciertas cosas, por lo tanto, hay escenarios donde es mejor listas y en otras árboles, así como hay situaciones donde una estructura es imposible de usar.
Las unidades dentro de una estructura tipo árbol son… Archivos , Carpetas, Directorios sIn archivos, Dispositivos externos que usan memorias aux para guardar información o ninguna de las anteriores. Me podrías sacar la duda de ésto??
Si te refieres a como está estructurado el sistema de archivos.. cada unidad sería un árbol independiente, donde cada archivo o carpeta será un nodo por igual, la única diferenncia es que su contenido es diferente, de esta forma, un archivo siempre sería una hoja, mientras que una carpeta podría ser una hoja o una rama, todo dependería de si tiene archivos o no
saludos.
La altura no esta mal en el ejemplo? El nivel raiz no se deberia contar como 0?
Bueno, depende como lo veas, si lo ves como código pues si, pero si es para explicar los niveles yo creo que está bien, pero bueno, creo que es lo de menos, al final creo que se entiende la idea
Gracias por la respuesta, solo era una duda especifica que tenia, pero si, para plantear la idea sin pasar a mayores razgos es entendible. Buen dia!
😀
Hola, conoces un algoritmo para calcular la longitud de camino interno de un árbol binario, creeme he intentado de todo y buscado en todos lados y no encuentro nada.
Hola Edsersson, no comprendí lo que quieres decir con longitud de camino interno
Hola Oscar
te agradezco me sacaste de algunas dudas que tenia sobre el tema explicas super
saludos
Me alegra que te sirvío, te mando un saludo 😀
Buen día, Óscar:
Primero que todo, felicitaciones por tu excelente contenido.
Cordialmente te solicito permiso para utilizar algunas imágenes de este artículo en un curso virtual de estructuras de datos elaborado por el Instituto Tecnológico Metropolitano (ITM) de Medellín (Colombia).
Claramente, las imágenes se citarían como corresponde y en cada una de ellas se remitiría al estudiante a tu página web.
Quedo atento y de antemano muchas gracias,
Juan David Gil Villa
Corrector de estilo
Instituto Tecnológico Metropolitano (ITM)
Medellín, Colombia
Hola Juan, claro adelante, toma lo que necesites.
saludos.
Hola que tal puedes hacer el Arbol de grado 2 con Backend Java y Angular ?
Los Árboles los puedes hacer en cualquier lenguaje
una pregunta, al momento de sacar la amplitud, si lo estoy escribiendo en un cuadro simplemente se colocan las letras en el orden de izquierda a derecha? o debe dar algun resultado ??
por ejemplo en un problema que me pongan a resolver
Hola Miguel, la aplitud es lo ancho del árbol, no comprendo bien tu pregunta
Hola buenas, como seria la implementacion del árbol general pero con nodos que tenga solo 3 atributos que son; la información del nodo, el hijo izquierdo, y el hermano derecho. Saludos
Pues eso, tendrías que crear una clase que tenga esos 3 tributos, no sabría que más decirte.
¿Como podría implementar un método para que muestre los nodos de un nivel especificamente?
Investiga sobre el recorrido en anchura, o por niveles, se basa en una Queue para resolver este problema.
SOY EL PROFESOR FEDERICIO DE COLOMBIA( WHASTAAP): +573146571313
Me parecio EXCELENTE ESTE MATERIAL, FELICITACIONES.
PUEDO AYUDAR A RESOLVER EJERCICIOS DE ESTE TEMA.
GRACIAS Y BENDICIONES
Hola Federico, pues dejo tus datos aquí por si alguien se quiere comunicar con usted para resolver algún ejercicios.
Hola Federico tu me puedes ayudar con un ejercicio?
•Realizar
un programa que muestre en pantalla el árbol binario de la imagen en java, (solicitar al usuario los valores para llenar el árbol).
•Luego hacer
un recorrido
por el árbol, en
orden, pre-orden y post-orden, y presentar en pantalla los
resultados de cada recorrido.
Hola me gustaría saber como puedo sacar el grado de un árbol, el concepto me quedo muy claro pero tengo ciertos problemas con el código.
mmmm, pues es relativamente simple, tendrás que crear una función recursiva que recorra todo el árbol y por cada elemento recorido, hay que comprobar el número de hijos, de esta forma, la función recursiva debe de regresar siempre el número mayor de hijos encontrado.
hola
de casualidad tendras un comparativo entre la busqueda de el valor minimo en un array mediante pilas o colas vs un arbol segmente tree
Muchas gracias por tu ayuda, me sirvio mucho el material.
No la raíz el el nivel 0?
Yo sabía que la raíz era nivel 0, por lo tanto en la figura 4, la altura es 3.
¿Es posible reconstruir el árbol a partir de solamente su recorrido en
posorden?
Por supuesto, es la forma en que un árbol se persisten, se guarda en un orden y luego se reconstruye al momento de leerse.
Excelentes explicaciones, muy buenas, y muy gráficas. Ayudan mucho a afianzar los conceptos.
Lastima que no tengas en el blog alguna opcion que permite imprimrlo directamente en PDF, me encantaria poder imprimirlas y guardarlas en una carpeta donde guardo todos los apuntes (si, ya se que soy un poco chapado a la antigua, pero me resulta mucho mas practico tenerlo impreso… y aunque pueda imprimir una pagina web, no queda bien…)