 Hace ya un tiempo atrás, cuando aún era estudiante de universidad. Estaba en 3° semestre y cursaba la asignatura de Estructura de Datos. Para no hacer el cuento largo, me dejaron realizar un proyecto muy interesante. Teníamos que desarrollar el algoritmo recursivo que resolviera el problema de las torres de Hanói. El proyecto era simple, desarrollar un algoritmo que fuera imprimiendo en pantalla el número de movimientos que iba realizando y el disco que movía en cada paso. Hasta aquí todo pintaba simple. Pero como siempre a mí me gustaba batallar y me arriesgue a desarrollar este proyecto de forma gráfica. Mi intención era impresionar a mi maestra y sí que lo logre, este proyecto fue suficiente para exentar un parcial :).
Hace ya un tiempo atrás, cuando aún era estudiante de universidad. Estaba en 3° semestre y cursaba la asignatura de Estructura de Datos. Para no hacer el cuento largo, me dejaron realizar un proyecto muy interesante. Teníamos que desarrollar el algoritmo recursivo que resolviera el problema de las torres de Hanói. El proyecto era simple, desarrollar un algoritmo que fuera imprimiendo en pantalla el número de movimientos que iba realizando y el disco que movía en cada paso. Hasta aquí todo pintaba simple. Pero como siempre a mí me gustaba batallar y me arriesgue a desarrollar este proyecto de forma gráfica. Mi intención era impresionar a mi maestra y sí que lo logre, este proyecto fue suficiente para exentar un parcial :).
La intención de este post es simplemente compartir con ustedes este proyecto, que lejos de ser una joya de la ingeniería de software, represento y sigue representando para mí un gran triunfo, pues fue desarrollado casi a los inicios de mi carrera. Sin experiencia, y claro, sin conocer nada de técnicas de ingeniería, patrones y arquitectura de software. Lo que busco con este post es compartir con todos este proyecto y que les pueda servir de ayuda, ya sea para simplemente comprender como funciona el algoritmo, curiosidad o para realizar su proyecto universitario.
En fin… antes de entrar a mi proyecto me gustaría repasar la teoría para todos aquellos que no están familiarizados con el juego de las torres de Hanói.
Las reglas:
El juego es simple. Se parte de un tablero que tiene 3 estacas y ocho discos de tamaños distintos. Cada disco más grande que el anterior y colocados en la estaca inicial de la más grande a la más pequeña como se puede apreciar en la siguiente imagen:

El objetivo del juego es pasar todos los discos de la estaca inicial a la estaca final moviendo un disco en cada turno. La regla principal es que NUNCA podrás colocar un disco más grande sobre un disco más pequeño. Por lo que deberás utilizar la estaca auxiliar (La que no es la inicial ni la final) para ayudarte a mover los discos hasta la estaca final.

En la imagen, podemos apreciar el juego de las torres de Hanói con 4 discos. Nótese que el juego de mesa original está conformado por 8 discos aunque existen modelos con más o menos discos, lo único que no varía es el número de estacas.
Bien. Una vez que todos los discos se encuentran en la estaca final correctamente ordenados de mayor a menor el juego ha terminado. Es importante destacar que no existe un número máximo de movimientos. Sin embargo, existe una fórmula para determinar el número mínimo de movimientos para resolver el juego: la fórmula es 2n – 1, donde n es el número de discos. Por ejemplo para resolver el juego con 4 discos como aparece en la imagen anterior, la formular quedaría de la siguiente manera (2 ^ 4) – 1 = 15 . Lógicamente entre más discos el número de movimientos crecerá de forma exponencial y se requerirán de muchos más movimientos para resolver el juego.
Algoritmo de las Torres de Hanói:
En las univercidades es muy comun encontrar que piden solucionar este problema como parte de proyectos o trabajos, en algunos casos, el problema pide ser resulto desde cero, en otras, el profesor brinda un borrador del algorimo y en otros casos dan una versión del algoritmo con un pequeño bug, el cual debe de ser en encontrado y resuelto. En cualquier caso, el resultado deberá ser el mismo, lograr que todos los discos pasen de la estaca inicial a la final siguiendo las reglas.
Existe dos formas de solucionar este problema, de forma iterativa y recursiva. En este caso trataremos únicamente la solución recursiva, pues es la que utilizo en el proyecto.
Algoritmo Torres de Hanói (Complejidad 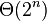 ) ) |
Entrada: Tres pilas de números origen, auxiliar, destino, con la pila origen ordenadaSalida: La pila destino
|
Este algoritmo puede resultar enredoso pero una vez que lo analizamos nos daremos cuenta que no lo es tanto.
El proyecto “Torres de Hanói“:
Bueno, ya con una breve introducción al juego de las torres de Hanói les enseñare mi proyecto. Además puedes descargar el código fuente del siguiente repositorio de GitHub . Recuerda que puede leer mi post hacer de las diferencias entre Git y Subversión aquí.
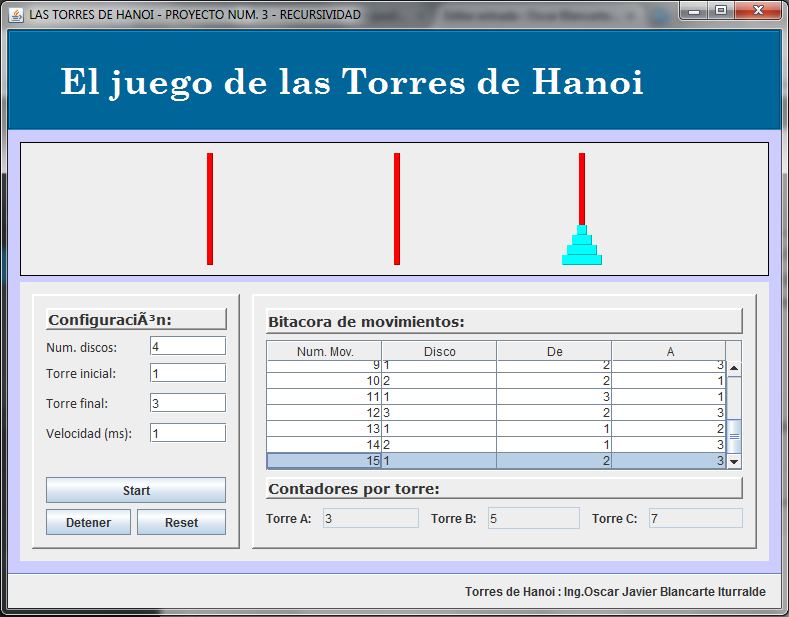
Para utilizar el juego es muy simple. Primero que nada es necesario introducir en el primer campo el número de discos con el que jugaras, el cual deberá ser mayor que 1, Lo siguiente es especificar la estaca inicial y la final los cuales deberán ser valores numéricos en el rango de 1 a 3. Finalmente especificamos la velocidad con la que se realizarán los movimientos, la velocidad esta expresada en milisegundos y a menor sea el tiempo, más rápido se resolverá el problema. Como nota, una configuración adecuada es la de 8 discos, estaca inicial y final 1 y 3 respectivamente y una velocidad de 1000 (1 segundo).

Como verán, el objetivo de este artículo no es el de explicar a fondo la teoría ni el fundamento del algoritmo de las torres de Hanói, en su lugar es compartir este pequeño proyecto que desarrolle y se me hico interesante compartirles.
Recuerda que te puedes suscribir para recibir todas las notificaciones de mi blog.

 entonces
entonces ,origen,destino, auxiliar) //mover todas las fichas menos la más grande (n) a la varilla auxiliar
,origen,destino, auxiliar) //mover todas las fichas menos la más grande (n) a la varilla auxiliar
La magia de la recursividad. Una llamada recursiva con parámetros de prioridad permite simular el juego de las torres de hanoi. ¿Qué computadora es mas rápida? ¿Qué relación tiene un recorrido infijo con la función recursiva de las torres de hanoi?
Hola Buenos dias
me gustaria saber como poder resolver este problema de las Torres de Hanoi consiste en un conjunto de N piezas de diferentes tamaños superpuestas en una pila A donde la más alta siempre es inferior en tamaño a la predecesora.
Se desea trasladar a la posición C las piezas de una en una usando para ello la posición B y respetando la norma de que no es posible colocar sobre una pieza más pequeña una de mayor tamaño.
Considere para el caso tantas variables o datos como sean necesarios para alcanzar la solución.
Desarrolle un programa de robot en V+ que resuelva el problema aplicado a la torre de tamaño N=3.
Si alguien me ayuda le estaré agradecido.
Muchas Gracias